Implementing a MLP with numpy
Motivation
During my deep learning class of 2023, we were asked to build from a MLP with numpy. We trained the multilayer perceptron with the MNIST dataset.The goal was to develop a primitive but working implementation of a MLP with the help of Numpy. I won’t go over the exact details of the experimentation. The experimentation was originally coded in a colab notebook.
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
import random
sns.set()
if __name__ == "__main__":
# load data
from tensorflow.keras.datasets import mnist
(x_train, y_train), (x_test, y_test) = mnist.load_data()
Implementing a single Perceptron with NumPy
The perceptron function is defined as:
\[\begin{equation} f(x) = \begin{cases} 1 \text{ if } w \cdot x+b > 0 \\ 0 \text{ otherwise} \end{cases} \end{equation}\]In the section below, we are implementing a perceptron with the ReLu activation function and the absolute loss function.
class BinaryPerceptron:
def __init__(self, input_dim):
'''
Initialize perceptron with random parameters
'''
self.w = np.random.randn(input_dim)
self.b = 0
def relu(self, x):
'''
Implement the ReLu function
:param x: input tensor
:return: x after ReLu function
'''
zeros = np.zeros_like(x)
# return ...
return np.maximum(x,zeros)
def fire(self, x):
'''
function determining whether perceptron is activated/fired given stimulus x.
(Corresponds to f(x) above)
:param x: input tensor
:return: 1 if perceptron is fired, 0 otherwise
'''
# o = ...
o = np.dot(self.w,x)+self.b
a = self.relu(o).item(0)
return 1 if a > 0 else 0
def train(self, x, y, lr):
'''
Manual implementation of the backpropagation algorithm
:param x: input vector x
:param y: target label y
:param lr: learning rate
:return: l1 loss
'''
y_hat = self.fire(x)
diff = y - y_hat
# gradient_w
zeros = np.zeros_like(x)
sgn = np.sign(diff)
grad_w = -sgn*np.maximum(zeros, x)
# gradienb_b
grad_b = -sgn*np.ones_like(x)
# update self.w
self.w = self.w - lr* grad_w
# update self.b
self.b = self.b - lr* grad_b
loss = np.abs(diff)
return loss
The following section is devoted to training our new Perceptron on a synthethic binary classification dataset, using a learning rate of 0.001. The model is trained for 3 epochs.
if __name__ == "__main__":
# Generate binary synthetic data and define graph function
# 100 data points of class 0 centered at (-5, -5)
# 100 data points of class 1 centered at (5, 5)
num_samples = 100
np.random.seed(42)
X_class0 = np.random.randn(num_samples, 2) + np.array([-5, 5])
np.random.seed(42)
X_class1 = np.random.randn(num_samples, 2) + np.array([5, 5])
X = np.vstack([X_class0, X_class1])
y = np.hstack([np.zeros(num_samples), np.ones(num_samples)])
np.random.seed(42)
shuffle_idx = np.random.permutation(len(X))
X = X[shuffle_idx]
y = y[shuffle_idx]
def graph(X, y, perceptron, title):
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Paired, label="Data points")
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.1),
np.arange(y_min, y_max, 0.1))
Z = np.array([perceptron.fire(np.array([x, y])) for x, y in np.c_[xx.ravel(), yy.ravel()]])
Z = Z.reshape(xx.shape)
plt.contourf(xx, yy, Z, alpha=0.3, cmap=plt.cm.Paired, levels=[-1, 0, 1])
plt.title(title)
plt.show()
# Train the perceptron
num_epochs = 3
perceptron = BinaryPerceptron(input_dim=2)
for i in range(num_epochs):
losses = []
for j in range(num_samples * 2):
print(perceptron.w)
loss = perceptron.train(x = X[j], y = y[j], lr = 0.001)
losses.append(loss)
graph(X, y, perceptron, f'Perceptron Decision Boundary after epoch {i + 1}')
print(f" accuracy after epoch {i + 1}: ", sum(1 for loss in losses if loss == 0) / (num_samples * 2))
Here is the resulting decision boundary:
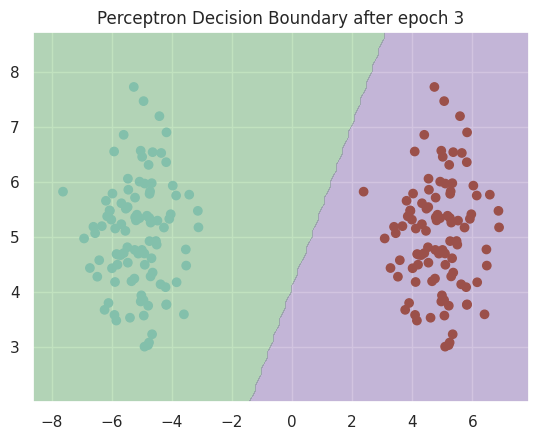
Our classifier was able to have 100% accuracy. In the real world, such results are unlikely as this training set was simple: it is linearly separable.
Implementing MLPs with NumPy
Multilayers perceptron are nothing more than a stack of Perceptrons. This simple idea allows to build much more complex decision boundary, thanks to the nonlinearity added by the activation function. The following code results in a ‘homemade’ numpy MLP.
\[\begin{aligned} \mathbf{o_{l+1}} &= \mathbf{W_l} \cdot \mathbf{a_l} + \mathbf{b_l} \\ \mathbf{a_{l+1}} &= \mathbf{a(o_{l+1})}, \end{aligned}\]where $\mathbf{o_{l+1}}$ is the preactivation output of the next layer, $\mathbf{a_{l+1}}$ is the output of the next layer. For the first/input layer, $\mathbf{a_l}$ is the input. For the last/output layer, we use the softmax activation function paired with cross-entropy loss.
import math
class MLP(object):
def __init__(self,
layer_dims = (784, 128, 64, 10),
activation = "relu",
epsilon = 1e-6,
lr = 0.01
):
super().__init__()
assert activation in ["relu", "sigmoid", "tanh"], "activation function needs to be among relu, sigmoid, tanh."
self.layer_dims = layer_dims
self.activation = activation
self.epsilon = epsilon
self.lr = lr
self.init_parameters()
def init_parameters(self):
'''
Initialize model parameters
'''
self.parameters = []
for i, layer_dim in enumerate(self.layer_dims[:-1]):
#w_shape = (self.layer_dims[i+1], layer_dim)
w_shape = (layer_dim , self.layer_dims[i+1] )
w = np.random.uniform(-1/math.sqrt(self.layer_dims[0]),1/math.sqrt(self.layer_dims[0]),w_shape)
# b =
b = np.zeros((1,self.layer_dims[i+1]))
self.parameters.append({f'w' : w, f'b' : b})
def activation_fn(self, x):
'''
Implementation of relu, sigmoid and tanh activation functions
:param x: input (preactivation) vector
:return: input after activation function
'''
if self.activation == "relu":
return np.maximum(0, x)
elif self.activation == "sigmoid":
return np.divide(np.ones_like(x) , (np.ones_like(x) + np.exp(-x)))
elif self.activation == "tanh":
return np.tanh(x)
def gradient_activation_fn(self, x):
'''
Implementation of the derivative function of the relu, sigmoid and tanh activation functions
:param x: input (postactivation) vector
:return: input after derivative of activation function
'''
if self.activation == "relu":
return np.where(x <= 0, 0, 1)
elif self.activation == "sigmoid":
return (1 - self.activation_fn(x))*self.activation_fn(x)
elif self.activation == "tanh":
return 1-np.power(self.activation_fn(x), 2)
def softmax(self, x):
'''
Implement code for the softmax function.
:param x: input vector
:return: vector with probabilities after softmax
'''
z = x - np.max(x, axis=-1, keepdims=True)
numerator = np.exp(z)
denominator = np.sum(numerator, axis=-1, keepdims=True)
softmax = numerator / denominator
return softmax
def layer_forward(self, x, layer_number):
'''
Implement code for forward/inference for the current layer
:param x: input vector to the current layer
:return: output vector after the current layer
'''
w = self.parameters[layer_number]['w']
b = self.parameters[layer_number]['b']
# pass
# o =
o = x @ w +b
if layer_number == len(self.parameters) - 1:
# a =
a = self.softmax(o)
else:
# a =
a = self.activation_fn(o)
self.forward_cache.append({'o' : o, 'a' : a})
return a
def forward(self, x):
'''
Apply layer_forward across all layers.
:param x: input vector to first layer
:return: output vector at the output layer
'''
self.forward_cache = [{'a' : x}]
y_hat = x
for i in range(len(self.parameters)):
# y_hat = ...
y_hat = self.layer_forward(y_hat, i)
return y_hat
def cross_entropy_loss(self, y_hat, y):
'''
Implement cross-entropy loss for classification
:param y_hat: model predictions
:param y: true labels
:return: cross-entropy loss between y and y_hat
'''
y_hat[np.where(y_hat < self.epsilon)] = self.epsilon
y_hat[np.where(y_hat > 1 - self.epsilon)] = 1 - self.epsilon
# loss = ...
loss = - np.sum(y * np.log(y_hat))/y.shape[0]
return loss
def layer_backward(self, gradient, layer_number):
'''
Implementation of backpropagation for the current layer.
It only calculates the gradients and does not perform updates.
:param gradient: if output layer: gradient of current layer's preactivation output (gradient_o) w.r.t. loss
if other layers: gradient of current layer's postactivation output (gradient_a) w.r.t. loss
:param layer_number: index of the current layer
:return: (gradient of previous layer's output w.r.t loss,
gradient of current layers' weights w.r.t loss,
gradient of current layers' biases w.r.t. loss)
'''
a = self.forward_cache[layer_number]['a']
a_prev = self.forward_cache[layer_number - 1]['a']
w = self.parameters[layer_number - 1]['w']
if layer_number == len(self.layer_dims):
gradient_o = gradient
else:
# gradient_o = ...
gradient_o = self.gradient_activation_fn(a) * gradient
# gradient_w = ...
gradient_w = np.dot( a_prev.T, gradient_o)/a_prev.shape[0]# a_prev?
# gradient_b = ...
gradient_b = np.sum(gradient_o, axis = 0, keepdims = True)/a_prev.shape[0]
# gradient_a_prev = ...
gradient_a_prev = gradient_o*self.gradient_activation_fn(a) @ w.T # OK!
return gradient_a_prev, gradient_w, gradient_b
def backward(self, y_hat, y):
'''
Implementation of backpropagation. It takes the gradients from 'layer_backwards' and perform updates on weights and biases.
:param y_hat: model predictions
:param y: true labels (one-hot format)
'''
gradient = y_hat - y
for i in range(len(self.parameters), 0, -1):
gradient, gradient_w, gradient_b = self.layer_backward(gradient, i)
# self.parameters[i - 1]['w'] -= ...
self.parameters[i-1]['w'] -= self.lr * gradient_w
# self.parameters[i - 1]['b'] -= ...
self.parameters[i-1]['b'] -= self.lr * gradient_b
@staticmethod
def one_hot_encode(labels, num_classes):
'''
Implementation of one-hot encoding
:param labels: vector with class indexes
:param num_classes: number of classes in the one-hot encoding
:return: 2d array of one-hot encoded labels
'''
encoded = []
for input in labels:
encoded_input = np.zeros(num_classes)
encoded_input[input] += 1
encoded.append(encoded_input)
return np.array(encoded)
def train(self, x, y, batch_size=64, num_iterations=None):
'''
Implementation of MLP model training. It also automatically graphs training results.
:param x: batch inputs
:param y: batch labels (one-hot encoded)
:param batch_size: batch size
:param num_iterations: number of iterations to train the model (in batches).
If left None, the model will train for 1 epoch across all data.
'''
def graph_loss_and_accuracy(losses, accuracies):
iterations = np.arange(len(losses)) + 1
fig, ax1 = plt.subplots()
color_ax1 = 'cyan'
color_ax2 = 'pink'
linewidth = 0.2
ax1.set_xlabel('iterations')
ax1.set_ylabel('cross entropy loss', color=color_ax1)
ax1.plot(iterations, losses, color=color_ax1, linewidth=linewidth)
ax1.tick_params(axis='y', labelcolor=color_ax1)
ax2 = ax1.twinx()
ax2.set_ylabel('accuracy on training set', color=color_ax2)
ax2.plot(iterations, accuracies, color=color_ax2, linewidth=linewidth)
ax2.tick_params(axis='y', labelcolor=color_ax2)
plt.show()
self.losses = []
self.accuracies = []
num_batches = x.shape[0] // batch_size
# train 1 epoch by default
if num_iterations is None: num_iterations = num_batches
for i in range(num_iterations):
start_idx = i * batch_size
end_idx = start_idx + batch_size
x_batch = x[start_idx : end_idx]
y_batch = y[start_idx : end_idx]
y_hat_batch = self.forward(x_batch)
loss = self.cross_entropy_loss(y_hat_batch, y_batch)
accuracy = np.sum(y_hat_batch.argmax(axis=-1) == y_batch.argmax(axis=-1)) / batch_size
self.losses.append(loss)
self.accuracies.append(accuracy)
self.backward(y_hat_batch, y_batch)
graph_loss_and_accuracy(self.losses, self.accuracies)
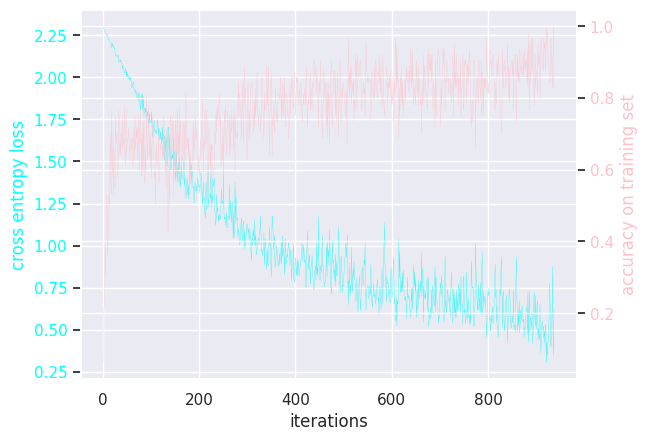
Here is the (hidden) training loops:
if __name__ == "__main__":
x_train_mlp = x_train.reshape(x_train.shape[0], -1)
y_train_mlp = MLP.one_hot_encode(y_train, 10)
# Batch sizes of 16, 32, 64, 128 respectively, default learning rate and activation function
mlp16 = MLP()
print("MLP batch size = 16")
mlp16.train(x_train_mlp, y_train_mlp, batch_size = 16)
mlp32 = MLP()
print("MLP batch size = 32")
mlp32.train(x_train_mlp, y_train_mlp, batch_size = 32)
mlp64 = MLP()
print("MLP batch size = 64")
mlp64.train(x_train_mlp, y_train_mlp, batch_size = 64)
mlp128 = MLP()
print("MLP batch size = 128")
mlp128.train(x_train_mlp, y_train_mlp, batch_size = 128)
# Learning rates of 0.1, 0.01, 0.001, 0.0001 respectively, default batch size and activation function
mlp1 = MLP(lr=0.1)
print("MLP learning rate = 0.1")
mlp1.train(x_train_mlp, y_train_mlp)
mlp2 = MLP(lr=0.01)
print("MLP learning rate = 0.01")
mlp2.train(x_train_mlp, y_train_mlp)
mlp3 = MLP(lr=0.001)
print("MLP learning rate = 0.001")
mlp3.train(x_train_mlp, y_train_mlp)
mlp4 = MLP(lr=0.0001)
print("MLP learning rate = 0.0001")
mlp4.train(x_train_mlp, y_train_mlp)
# Activation functions of "relu", "sigmoid" and "tanh" respectively, default learning rate and batch size
mlprelu = MLP(activation = "relu")
print("MLP activation relu")
mlprelu.train(x_train_mlp, y_train_mlp)
mlpsig = MLP(activation = "sigmoid")
print("MLP activation sigmoid")
mlpsig.train(x_train_mlp, y_train_mlp)
mlptanh = MLP(activation = "tanh")
print("MLP activation tanh")
mlptanh.train(x_train_mlp, y_train_mlp)
Results of modifying a few hyperparameters:
MLP batch size = 16
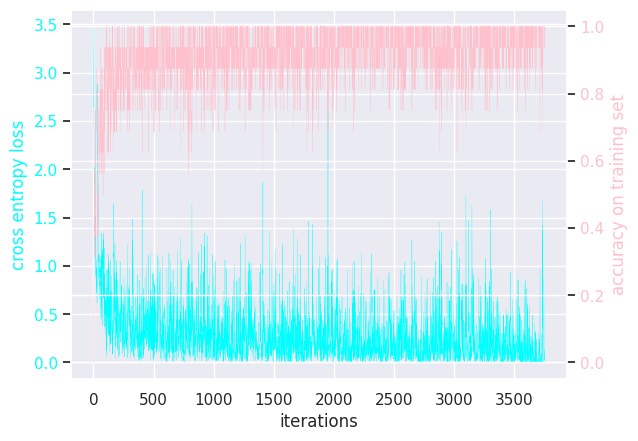
MLP batch size = 32
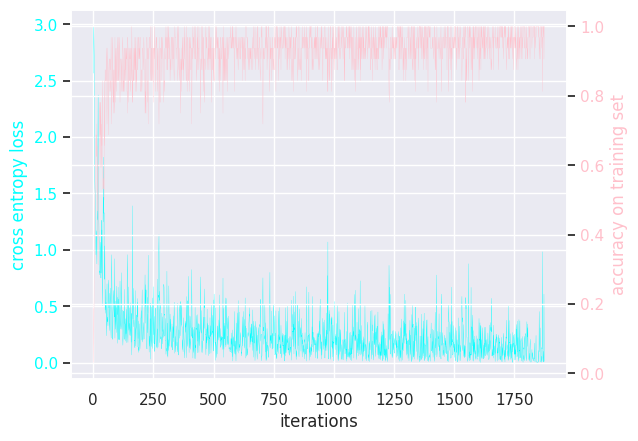
MLP batch size = 64
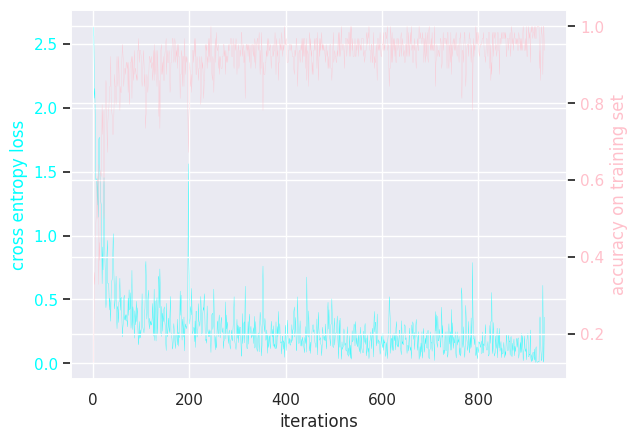
MLP batch size = 128
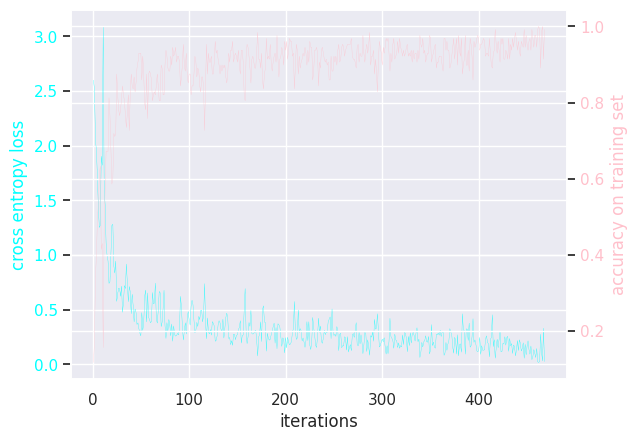
MLP learning rate = 0.1
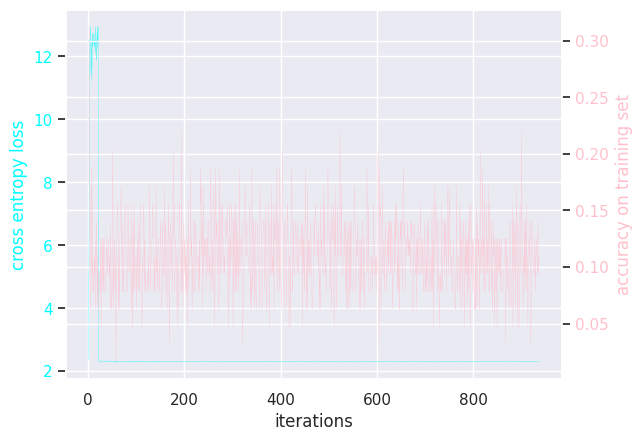
MLP learning rate = 0.01
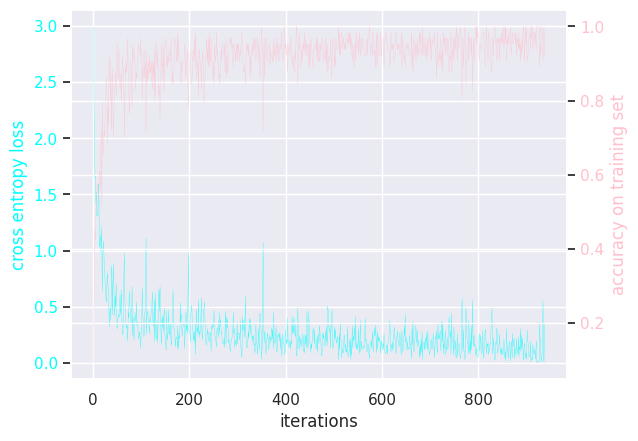
MLP learning rate = 0.001
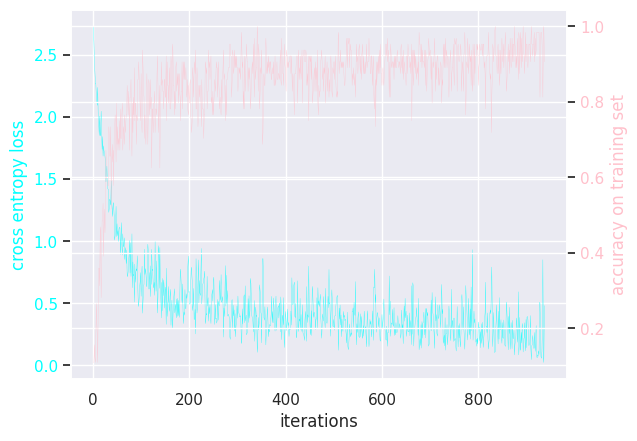
MLP learning rate = 0.0001
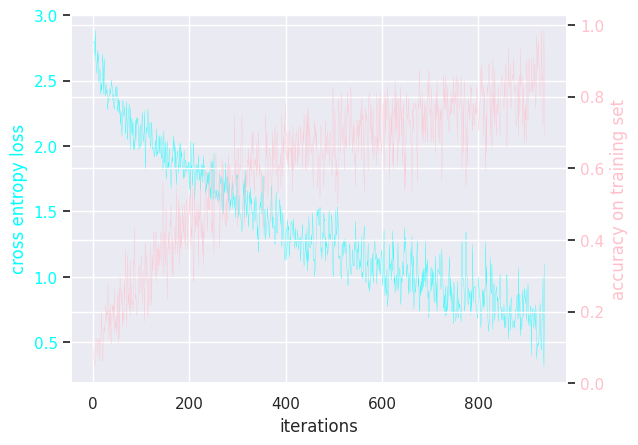
MLP activation relu
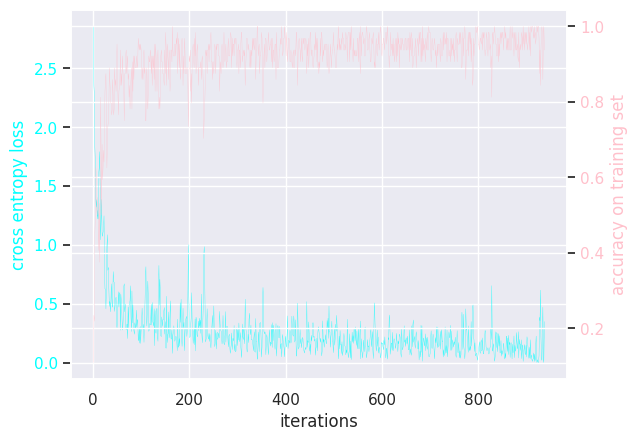
MLP activation sigmoid
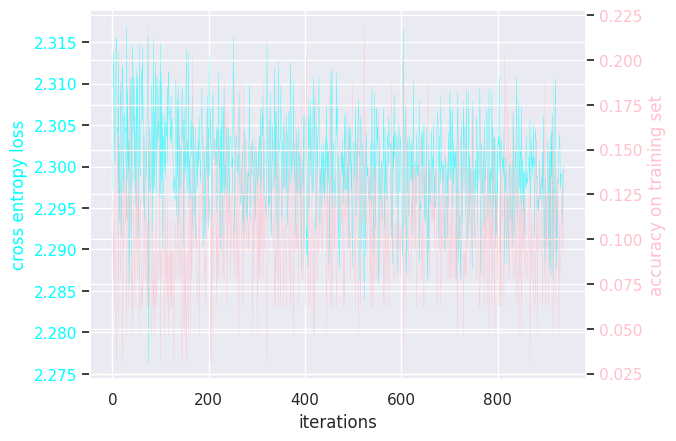
MLP activation tanh